Bachelorprojekte
Wir betrachten getriebene Quantensysteme, wie z.B. Materie in intensiven Laserfeldern, insbesondere die Quantendynmamik der Elektronen und das abgestrahlte Licht. Wir lösen dazu - mit gewissen Vereinfachungen - die zeitabhängige Schrödinger-Gleichung so gut wie möglich analytisch. Meist ist das Problem nicht vollständig analytisch lösbar und es bleibt ein Rest an Numerik. Oder man löst das Problem mit möglichst wenig vereinfachenden Annahmen numerisch und vergleicht mit den analytischen Lösungen des vereinfachten Modells.
Konkrete Bachelorarbeitsthemen:
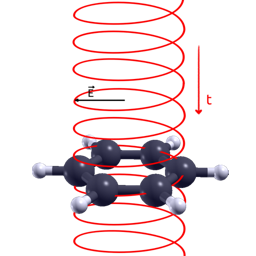
Betreuungsperson: Samuel Schöpa
Sprache: Deutsch/Englisch
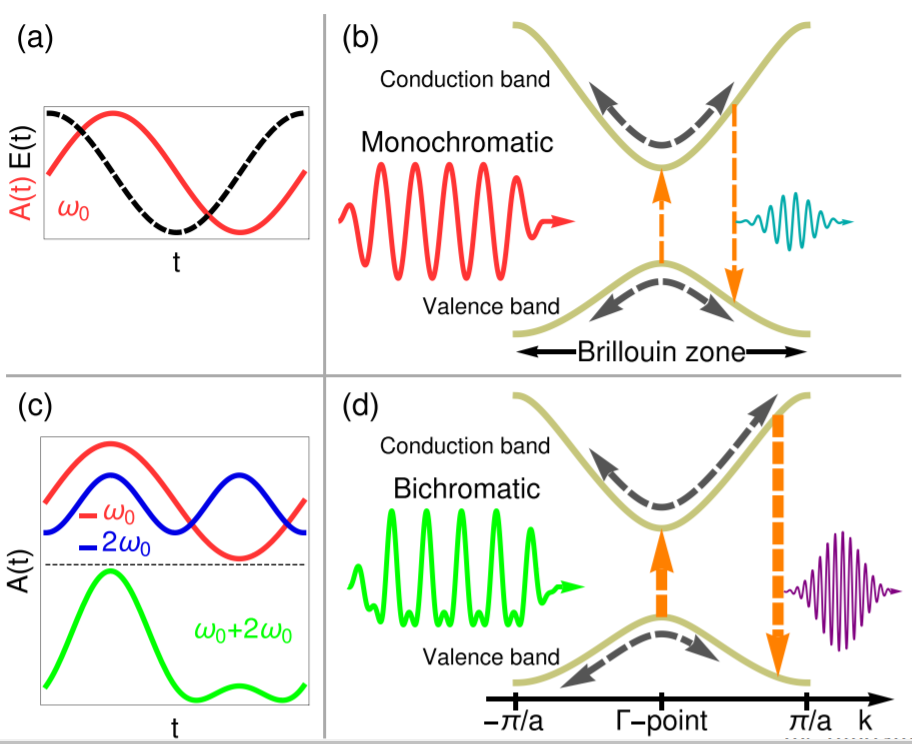
Die Erzeugung von hohen Harmonischen in dotierten Halbleitern mithilfe von zweifarbigen Laserpulsen
Betreuungsperson: Dr. Francisco Navarrete
Sprache: Deutsch/Englisch
Eine Einführung in topologische Isolatoren
Betreuungsperson: Gabriel Caceres-Aravena
Sprache: Englisch
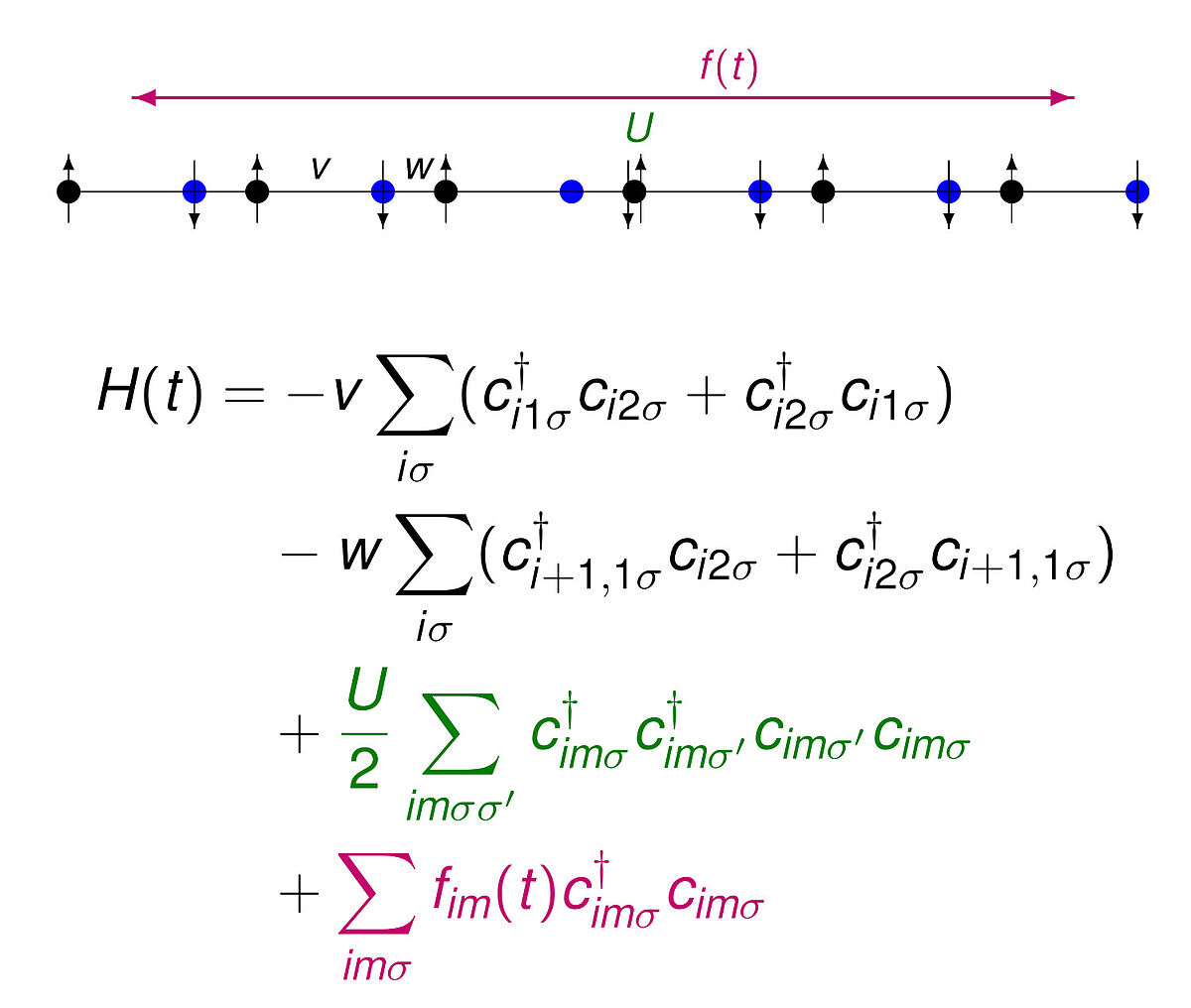
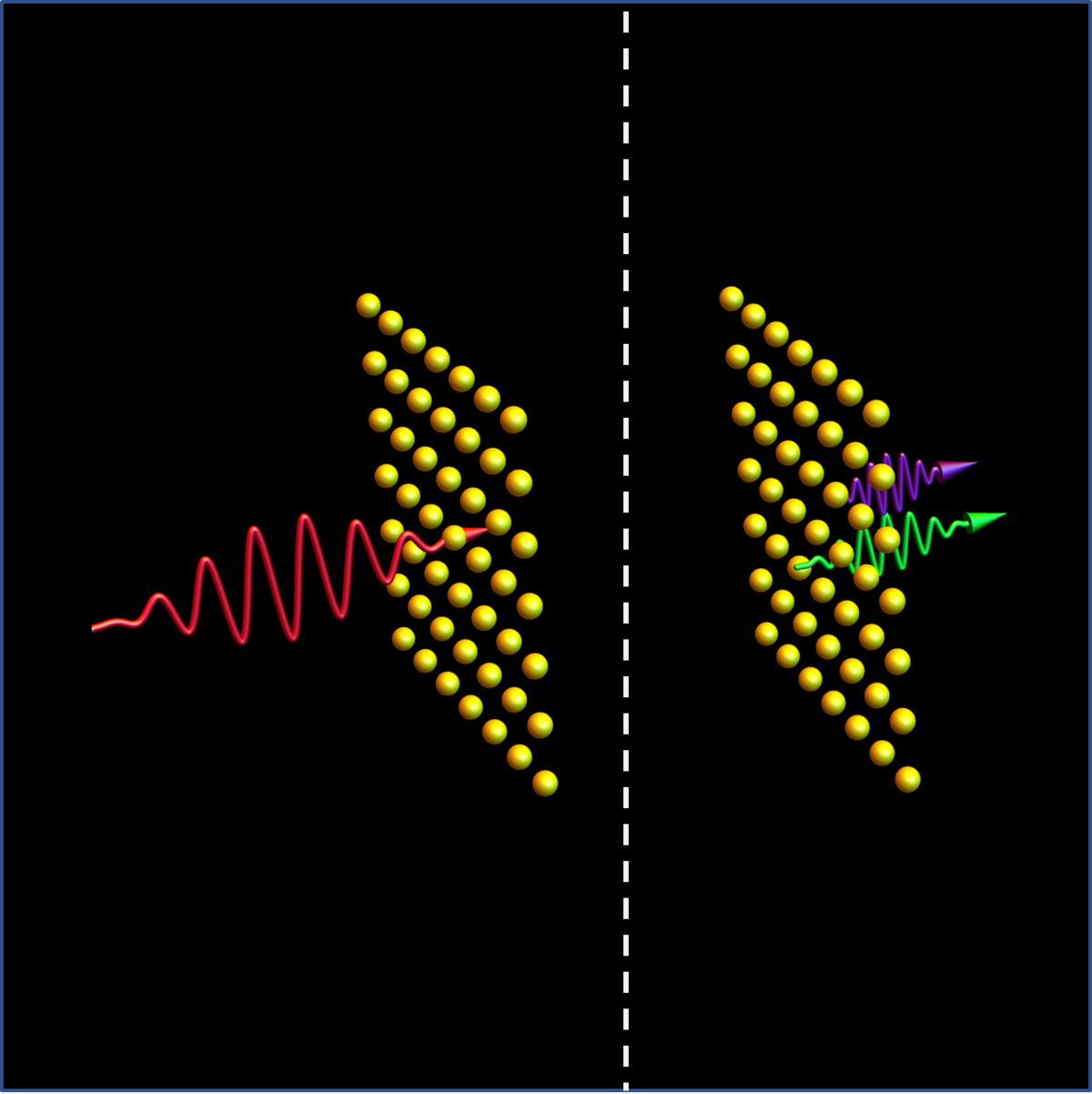
Hohe-Harmonischen-Erzeugung in topologischen Ketten mit Wechselwirkung
Betreuungsperson: Prof. Dieter Bauer
Sprache: Deutsch/Englisch
Auswahlregeln für Laser-Festkörper Wechselwirkung bei hohen Intensitäten
Betreuungsperson: Dr. Francisco Navarrete
Sprache: Deutsch/Englisch
Bei Interesse bitte per E-Mail an Herrn Professor Bauer einen individuellen Gesprächstermin vereinbaren.
Master Topics
Master projects are offered in the fields:
- Topological effects in strong-field laser-matter interactions
- High-harmonic spectroscopy of condensed matter and molecules
- Phase-controlled photoemission
- Topological effects in Floquet systems with interaction
Often, our Master students obtain results that are interesting enough to be published in international, refereed journals. Please check our publications.
Specific proposals:
Topology, Dispersion and Localization in SSH, Graphene and Bilayer Graphene
Supervisor: Gabriel Caceres-Aravena
Language: English

Supervisor: Samuel Schöpa
Language: English/German

High harmonic generation in doped semiconductors by two-color pulses
Supervisor: Dr. Francisco Navarrete
Language: English/German

High harmonic generation in topological chains with interaction
Supervisor: Prof. Dieter Bauer
Language: English/German
If you are interested, please contact Professor Bauer by e-mail to arrange an individual appointment.
Examensarbeiten
Wir bieten Staatsexamensarbeiten in folgenden Gebieten an:
Quantendynamik
(Prof. Dieter Bauer und Mitarbeiter/innen)
Die (zeitabhängige) Schrödingergleichung wird näherungsweise analytisch bzw. exakt numerisch gelöst. Untersucht werden jeweils exemplarisch fundamentale quantenmechanische Effekte (Tunneln, Interferenz, Verschränkung, geometrische Phasen etc.).